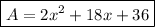Question

The length of a rectangular park is twice its width.

The park is surrounded by a 3-foot-wide path.
Write a quadratic function to represent the total
area of the park and the path.

Answer 1

`A=2x^2+18x+36`

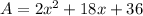
Explanation:

Quadratic Function

It's given the length of a rectangular park is twice its width.

Let's call:

x = width of the rectangular park

2x = length of the rectangular park

The park is surrounded by a 3-foot-wide path. This path adds 3 ft twice to both dimensions, i.e.:

x+3+3=x+6 width of the park and the path

2x+3+3=2x+6 length of the park and the path

The total area is:

A=(x+6)(2x+6)

Operating:

`A=2x^2+6x+12x+36`

`\boxed{A=2x^2+18x+36}`