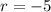Answer:
r = 1 and r = -5
Explanation:
We are given the following problem with an absolute value equation:

The only variable here is
 so we will make it the subject and solve for it.
so we will make it the subject and solve for it.

Isolating the absolute value by dividing the constant -12 by -2 to get:
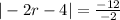
Setting the quantity inside the absolute value notation equal to a positive and a negative value on the other side of the equation:
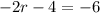 and
and
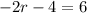
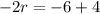 and
and

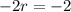 and
and
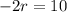
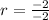 and
and
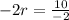
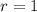 and
and