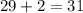The answer is: 29 and 31.
1. Let's call the smaller odd number:
 .
.
2. Let's call the larger odd number:
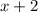
3. Based on the information given in the problem, the sum of the larger number (
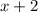 ) and twice the smaller number (
) and twice the smaller number (
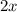 ) is 27 less than four times the smaller number (
) is 27 less than four times the smaller number (
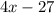 ).
).
4. Then, you can write the following expression and solve for
 to find the smaller number:
to find the smaller number:
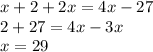
5. Therefore, the larger number is: