Question

Which of the following is an irrational number?

Answer 1

The answer is:

`\sf{√(18)}`

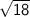
Work/explanation:

What are irrational numbers?

An irrational number is a number that cannot be expressed in the form of p/q, where q ≠ 0.

Note that terminating decimals are NOT irrational numbers.

So the first one is not an irrational number.

Let's consider the next one -
`\sf{(√(12))^2}`

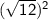
The square root and the square cancel each other out, and what is left is 12, which is a perfectly rational number.

Now we consider choice C, which is
`\sf{√(18)}`.

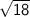This one is an irrational number, as it cannot be expressed in p/q form.

Finally, let's consider choice D.

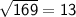`\sf{√(169)=13}`, which is rational too!

Hence,
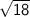`\sf{√(18)}` is irrational.

Answer 2

0.78 bar = 0.788888...

Note that the decimal expansion of an irrational number is non terminating and non repeating.

But, since the above decimal expansion is non terminating and repeating, this is not an irrational number.

`(√(12)) ^(2) =12` which is rational.

`√(169) =\sqrt{13^(2) } =13` and hence, a rational number

`√(18) =√(9(2)) =3√(2)` is an irrational number.