Question

In a basketball game, Tatiana made 23 baskets. Each of the baskets was worth either 2 or 3 points, and Tatiana scored a total of 53 points. Let x represent the number of two-point baskets she made and y represent the number of three-point baskets she made . Write a system of equations to represent the situation and solve the system to find out how many two point and three point baskets Tatiana made.

Answer 1

X+y=23 (x and y added equal the number of baskets made)

2x+3y=53 (since each basket is worth a certain amount of points, x and y must be multiplied by their amount of baskets and added together to get the total number of points)

Hope this helps!

Answer 2

Tatiana scored 7 three points baskets, and 16 two-points baskets.

Explanation:

Givens:

• Tatiana made 23 baskets.
• 
  `x` represents the two-point baskets.
• 
  `y` represents the three-point baskets.
• Tatiana scored 53 points.

The expression for the 23 baskets made by Tatiana would be:

`x+y=23`

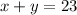
In words, the sum of both type of scored baskets sum 23.

The expression for the total points scored would be:

`2x+3y=53`

In words, baskets of two points and three points sum 53 total points scored by Tatiana.

Now, we isolate
`x` in the first equation and replace it in the second equation:

`x=23-y\\2(23-y)+3y=53\\46-2y+3y=53\\y=53-46\\y=7`

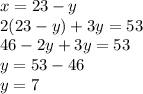
Replacing this value in the first equation, we have:

`x+y=23\\x=23-7=16`

Therefore, Tatiana scored 7 three points baskets, and 16 two-points baskets.