Question

Choose whether it's always, sometimes, never 

an integer added to an integer is an integer
a polynomial subtracted from a polynomial is a polynomial
a polynomial divided by a polynomial is a polynomial
a polynomial multiplied by a polynomial is a polynomial

Answer 1

1) an integer added to an integer is an integer - Always

(adding two integers always results in an integer, if the two integers are positive, their sum will be positive, if two integers are negative, they will yield a negative sum)

2) a polynomial subtracted from a polynomial is a polynomial - Always

(if the polynomials are subtracted vertically, then the signs of the subtracted polynomial's need to be flipped to their opposites)

3) a polynomial divided by a polynomial is a polynomial - Sometimes

(this depends on the degree of polynomials in the numerator and the denominator)

4) a polynomial multiplied by a polynomial is a polynomial - Always

(when two polynomials are added, the product function is the addition of degree to both the polynomials)

Answer 2

Answer: An integer added to an integer is an integer, this statement is always true. A polynomial subtracted from a polynomial is a polynomial, this statement is always true. A polynomial divided by a polynomial is a polynomial, this statement is sometimes true. A polynomial multiplied by a polynomial is a polynomial, this statement is always true.

Step-by-step explanation:

1)

The closure property of integer states that the addition, subtraction and multiplication is integers is always an integer.

If
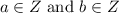`a\in Z\text{ and }b\in Z`, then a+b\in Z.

Therefore, an integer added to an integer is an integer, this statement is always true.

2)

A polynomial is in the form of,

`p(x)=a_nx^n+a_(n-1)x^(x-1)+...+a_1x+a_0`

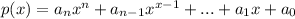
Where
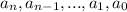`a_n,a_(n-1),...,a_1,a_0` are constant coefficient.

When we subtract the two polynomial then the resultant is also a polynomial form.

Therefore, a polynomial subtracted from a polynomial is a polynomial, this statement is always true.

3)

If a polynomial divided by a polynomial then it may or may not be a polynomial.

If the degree of numerator polynomial is higher than the degree of denominator polynomial then it may be a polynomial.

For example:

`f(x)=x^2-2x+5x-10 \text{ and } g(x)=x-2`

Then
`(f(x))/(g(x))=x^2+5`, which a polynomial.

If the degree of numerator polynomial is less than the degree of denominator polynomial then it is a rational function.

For example:

`f(x)=x^2-2x+5x-10 \text{ and } g(x)=x-2`

Then
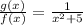`(g(x))/(f(x))=(1)/(x^2+5)`, which a not a polynomial.

Therefore, a polynomial divided by a polynomial is a polynomial, this statement is sometimes true.

4)

As we know a polynomial is in the form of,

`p(x)=a_nx^n+a_(n-1)x^(x-1)+...+a_1x+a_0`

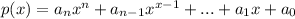
Where
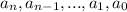`a_n,a_(n-1),...,a_1,a_0` are constant coefficient.

When we multiply the two polynomial, the degree of the resultand function is addition of degree of both polyminals and the resultant is also a polynomial form.

Therefore, a polynomial subtracted from a polynomial is a polynomial, this statement is always true.