 = 3
= 3
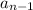 - 8, with
- 8, with
 = 7
= 7
generate the first few terms of the sequence
 = 3 + 4 = 7
= 3 + 4 = 7
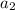 = 3² + 4 = 9 + 4 = 13
= 3² + 4 = 9 + 4 = 13
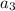 = 3³ + 4 = 237 + 4 = 31
= 3³ + 4 = 237 + 4 = 31
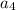 =
=
 + 4 = 81 + 4 = 85
+ 4 = 81 + 4 = 85
the sequence is 7, 13, 31, 85, .....
Checking the recursive formulae given the one that generates the sequence is
 = 3
= 3
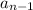 - 8 with
- 8 with
 = 7, as
= 7, as
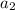 = (3 × 7 ) - 8 = 21 - 8 = 13 ← correct
= (3 × 7 ) - 8 = 21 - 8 = 13 ← correct
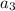 = (3 × 13 ) - 8 = 39 - 8 = 31 ← correct
= (3 × 13 ) - 8 = 39 - 8 = 31 ← correct
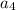 = (3 × 31 ) - 8 = 93 - 8 = 85 ← correct
= (3 × 31 ) - 8 = 93 - 8 = 85 ← correct