Answer:
40º
Explanation:
First, we need to graph the triangle.
The image attached shows that's a right triangle, where its right angle is placed at vertex S.
First, we need to find the length of sides RS and TS, then we apply trigonometric reasons to find both acute angles.
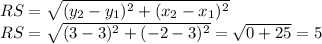
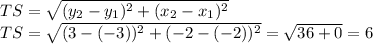
Now, we use the tangent reason to find both acute angles
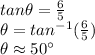
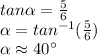
Therefore, the smallest angle rounded to the nearest degree is 40°.