Question

What is the measure to the nearest degree of the smallest angle in a triangle whose vertices are R(3, 3), S(-2, 3), and T(-2, -3)?

47º


40º


49º


51º

I got 50 but that isn't an option. 49?

Answer 1

check the picture below.

make sure your calculator is in Degree mode.

Answer 2

40º

Explanation:

First, we need to graph the triangle.

The image attached shows that's a right triangle, where its right angle is placed at vertex S.

First, we need to find the length of sides RS and TS, then we apply trigonometric reasons to find both acute angles.

`RS=\sqrt{(y_(2)-y_(1) )^(2) +(x_(2)-x_(1) )^(2) } \\RS=\sqrt{(3-3)^(2)+(-2-3)^(2) }=√(0+25) =5`

`TS=\sqrt{(y_(2)-y_(1) )^(2) +(x_(2)-x_(1) )^(2) } \\TS=\sqrt{(3-(-3))^(2)+(-2-(-2))^(2) }=√(36+0) =6`

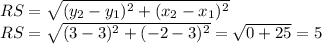
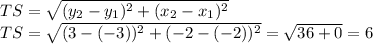
Now, we use the tangent reason to find both acute angles

`tan\theta=(6)/(5)\\ \theta=tan^(-1)((6)/(5) )\\ \theta \approx 50\°`

`tan\alpha=(5)/(6)\\ \alpha=tan^(-1)((5)/(6) )\\ \alpha \approx 40\°`

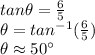
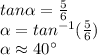
Therefore, the smallest angle rounded to the nearest degree is 40°.