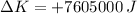Question

12. Unman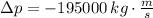ned Space Probe A 2500 kg unmanned space probe is moving in a straight line at a constant speed of 300 m/s. Control rock- ets on the space probe execute a burn in which a thrust of 3000 N acts for 65.0 s. (a) What is the change in the magnitude of the probe’s translational momentum if the thrust is backward, forward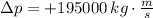, or di- rectly sideways? (b) What is the change in kinetic energy under the same three conditions? Assume that the mass of the ejected burn products is negligible compared to the mass of the space probe.

Answer 1

a) Backward -
`\Delta p = - 195000\,kg\cdot (m)/(s)`, Forward -
`\Delta p = + 195000\,kg\cdot (m)/(s)`, Directly sideways -
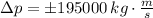`\Delta p = \pm 195000\,kg\cdot (m)/(s)`, b) Backward -
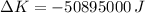`\Delta K = -50895000\,J`, Forward -
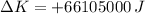`\Delta K = + 66105000\,J`, Directly sideways -
`\Delta K = + 7605000\,J`.

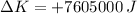Step-by-step explanation:

a) All scenarios are analyzed by means of the Principle of Momentum Conservation and the Impact Theorem.

Case I - Backward

`\Delta p = -(3000\,N)\cdot (65.0\,s)`

`\Delta p = - 195000\,kg\cdot (m)/(s)`

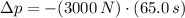
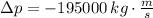
Case II - Forward

`\Delta p = +(3000\,N)\cdot (65.0\,s)`

`\Delta p = + 195000\,kg\cdot (m)/(s)`

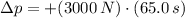
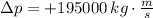
Case III - Directly sideways

`\vec p _(2)-\vec p_(1) = 0\,(kg\cdot m)/(s)\cdot i \pm 195000\, \,(kg\cdot m)/(s)\cdot j`

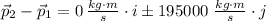
The magnitude of the change of the probe's translational momentum is:

`\Delta p = \pm 195000\,kg\cdot (m)/(s)`

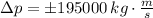
b) The change in kinetic energy is given by the Work-Energy Theorem:

Case I - Backward

The final speed of the probe is:

`v= 300\,(m)/(s)-\left((3000\,N)/(2500\,kg)\right)\cdot (65\,s)`

`v = 222\,(m)/(s)`

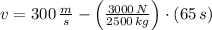
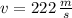
The change in kinetic energy is:

`\Delta K = (1)/(2) \cdot (2500\,kg)\cdot \left[(222\,(m)/(s) )^(2)-(300\,(m)/(s) )^(2) \right]`

`\Delta K = -50895000\,J`

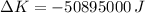
Case II - Forward

The final speed of the probe is:

`v= 300\,(m)/(s)+\left((3000\,N)/(2500\,kg)\right)\cdot (65\,s)`

`v = 378\,(m)/(s)`

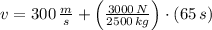
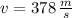
The change in kinetic energy is:

`\Delta K = (1)/(2) \cdot (2500\,kg)\cdot \left[(378\,(m)/(s) )^(2)-(300\,(m)/(s) )^(2) \right]`

`\Delta K = + 66105000\,J`

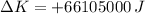
Case III - Directly sideways

The final speed of the probe in the direction perpendicular to the motion line is:

`v= 0\,(m)/(s)+\left((3000\,N)/(2500\,kg)\right)\cdot (65\,s)`

`v = 78\,(m)/(s)`

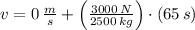
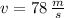
The change in kinetic energy is:

`\Delta K = (1)/(2) \cdot (2500\,kg)\cdot \left[(300\,(m)/(s) )^(2) + (78\,(m)/(s) )^(2) -(300\,(m)/(s) )^(2) \right]`

`\Delta K = + 7605000\,J`

Answer 2

answer of both parts are attached below