Question

A rectangular box has length x and width 3. The volume of the box is given by y = 3x(8 – x). The greatest x-intercept of the graph of this polynomial equals which of the following?

Choose all that apply.
The maximum possible width.
The maximum possible length.
The minimum possible height.
The maximum possible height.
The maximum possible volume.
 
(Can you also please tell me how you did it? I'm trying to learn. You don't have to though)

Answer 1

B, The maximum possible length, and C The minimum possible height.

Explanation:

Answer 2

Consider rectangular box with

• length x units (x≥0);
• width 3 units;
• height (8-x) units (8-x≥0, then x≤8).

The volume of the rectangular box can be calculated as

`V_(box)=\text{length}\cdot \text{width}\cdot \text{height}.`

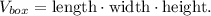
In your case,

`V_(box)=3\cdot x\cdot (8-x).`

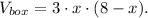
Note that maximal possible value of the height can be 8 units (when x=0 - minimal possible length) and the minimal possible height can be 0 units (when x=8 - maximal possible length).

From the attached graph you can see that the greatest x-intercept is x=8, then the height will be minimal and lenght will be maximal.

Then the volume will be V=0 (minimal).

Answer: correct choices are B (the maximum possible length), C (the minimum possible height)