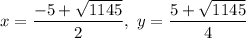Question

One positive number is 5 less than twice a second number, and their product is 140. Find the two numbers.

Answer 1

x, y - two positive numbers

one positive number is 5 less than twice a second number

(1) x = 2y - 5

their product is 140

(2) xy = 140

substitute from (1) to (2)

(2y - 5)y = 140 use distributive property

(2y)(y) - (5)(y) = 140

2y² - 5y = 140 subtract 140 from both sides

2y² - 5y - 140 = 0

use quadratic formula

a = 2, b = -5, c = -140

b² - 4ac = (-5)² - 4(2)(-140) = 25 + 1120 = 1145

`y_1=(-b-√(b^2-4ac))/(2a)\\\\y_1=(-(-5)-√(1145))/(2(2))=(5-√(1145))/(4) < 0`

`y_2=(-b+√(b^2-4ac))/(2a)\\\\y_2=(-(-5)+√(1145))/(2(2))=(5+√(1145))/(4)`

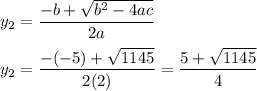
substitute the value of y₁ to (1)

`x=2\cdot(5+√(1145))/(4)-5=(5+√(1145))/(2)-(10)/(2)=(5+√(1145)-10)/(2)\\\\=(-5+√(1145))/(2)`

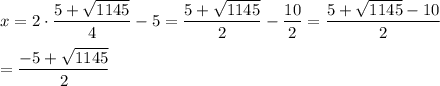
Answer:

`x=(-5+√(1145))/(2),\ y=(5+√(1145))/(4)`