Question

Which graph represents the function f(x)=x4+4x3−12x2−32x+64?

Answer 1

`f(x)=x^4+4x^3-12x^2-32x+64`

The degree of f(x) is 4. Also the leading coefficient is 1 and it is positive

So as x approaches infinity then y approaches infinity

as x approaches -infinity then y approaches infinity

The first and fourth graph goes up and it satisfies the above . so we ignore the second and third graph.

Now we check the x intercepts of the first graph

x intercepts of first graph is -4 and 2

Plug in -4 for x in f(x) and check whether we get 0

`f(x)=x^4+4x^3-12x^2-32x+64`

`f(x)=(-4)^4+4(-4)^3-12(-4)^2-32(-4)+64=0`

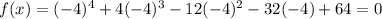
Now plug in 2 for x and check

`f(x)=(2)^4+4(2)^3-12(2)^2-32(2)+64=0`

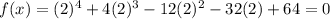
So -4 and 2 are the x intercepts that satisfies f(x)

Hence first option is the graph of
`f(x)=x^4+4x^3-12x^2-32x+64`

Answer 2

The function
`f(x)=x^4+4x^3-12x^2-32x+64 \\`

has a derivative

`f^\prime(x)=(x^3+4x^2-6x-8).\\`

The derivative of this function is zero when
`x=-4,x=-1,x=2.`

The derivative function is negative on the left side of -4 and positive on the right side, it is also negative on the right hand side of -1, and positive on the right hand side of positive 2. From this information we can gather that the graph of f(x) has a minima at x=-4, a maxima at x=-1 and a minima at x=-2.

The only graph that fits this description from the given ones is the first graph