
The degree of f(x) is 4. Also the leading coefficient is 1 and it is positive
So as x approaches infinity then y approaches infinity
as x approaches -infinity then y approaches infinity
The first and fourth graph goes up and it satisfies the above . so we ignore the second and third graph.
Now we check the x intercepts of the first graph
x intercepts of first graph is -4 and 2
Plug in -4 for x in f(x) and check whether we get 0

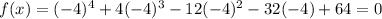
Now plug in 2 for x and check
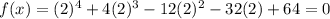
So -4 and 2 are the x intercepts that satisfies f(x)
Hence first option is the graph of
