Let the segment be represented by AB where A(0,0) =
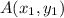 and B(3/4,9/10) =
and B(3/4,9/10) =
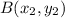 .
.
The length of the segment drawn by architect can be calculated using distance formula:
AB =

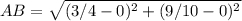
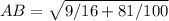
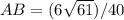
Similarly, Let the actual end points of segment be AC where A(0,0) =
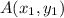 and C(30,36) =
and C(30,36) =
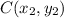 .
.
The length of the original segment can be calculated using distance formula:
AC =


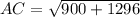
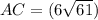 .
.
Thus, the actual length is 40 times the length of the segment drawn by the architect.
Thus, the proportion of the model is 1:40