Find the sum of the first six terms of the sequence for which a2=0.7 and a3=0.49.

Question

asked Nov 19, 2019 189k views

2 Answers

Coco Puffs · Answer 1 · 2019-11-24T18:11:36+0000

Answer: Sum of the first six terms is 2.31.

Explanation:

Since we have given that

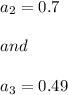
$a_2=0.7\\\\and\\\\a_3=0.49$

Since we know the formula for "Arithmetic Progression":

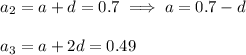
$a_2=a+d=0.7\implies a=0.7-d\\\\a_3=a+2d=0.49$

Now, solving the above two equations:

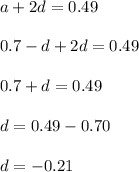
$a+2d=0.49\\\\0.7-d+2d=0.49\\\\0.7+d=0.49\\\\d=0.49-0.70\\\\d=-0.21$

So, when we put the value of d in the first equation, we get that

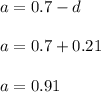
$a=0.7-d\\\\a=0.7+0.21\\\\a=0.91$

so, Sum of first six terms would be

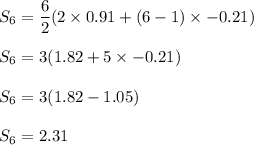
$S_6=(6)/(2)(2* 0.91+(6-1)* -0.21)\\\\S_6=3(1.82+5* -0.21)\\\\S_6=3(1.82-1.05)\\\\S_6=2.31$

Hence, Sum of the first six terms is 2.31.