Question

Find the sum of the first six terms of the sequence for which a2=0.7 and a3=0.49.

Answer 1

a1 = 0.91
a6 = -0.14
sum = (0.91+-0.14) /2
sum = 2.31

Answer 2

Answer: Sum of the first six terms is 2.31.

Explanation:

Since we have given that

`a_2=0.7\\\\and\\\\a_3=0.49`

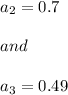
Since we know the formula for "Arithmetic Progression":

`a_2=a+d=0.7\implies a=0.7-d\\\\a_3=a+2d=0.49`

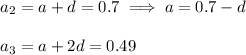
Now, solving the above two equations:

`a+2d=0.49\\\\0.7-d+2d=0.49\\\\0.7+d=0.49\\\\d=0.49-0.70\\\\d=-0.21`

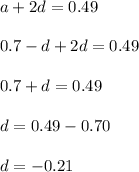
So, when we put the value of d in the first equation, we get that

`a=0.7-d\\\\a=0.7+0.21\\\\a=0.91`

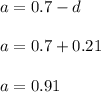
so, Sum of first six terms would be

`S_6=(6)/(2)(2* 0.91+(6-1)* -0.21)\\\\S_6=3(1.82+5* -0.21)\\\\S_6=3(1.82-1.05)\\\\S_6=2.31`

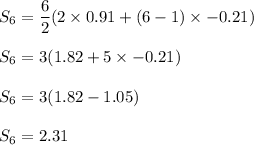
Hence, Sum of the first six terms is 2.31.