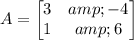As per the matrix theory the given system of equations can be written as:
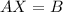 ....................(Equation 1)
....................(Equation 1)
Where, A is the Coefficient Matrix (always a square matrix),
X is the variables' matrix (always a column matrix), and
B is the Constant Matrix (again always a column Matrix).
Since our's is a two system equation in two unknowns, we will have the coefficient matrix as a 2x2 square matrix and the other two matrices will be 2x1 column matrices.
Thus, the given system in terms of matrices will be:
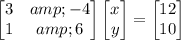
Comparing the above equation with (Equation 1) we can clearly see that the correct coefficient matrix of the given system is: