Let the winnings in dollars in the single play of a game be "X".
Thus, in our case the only three values that X can take is +4 (or 4), -2 and -6.
It is also given that
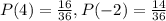 and
and
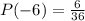 .
.
Therefore, the probability of losing money in a single play of the game will be the sum of the probability of the losses.
Thus,
 .
.
Thus, the approximate probability of losing money in one play of the game is
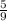 or 55.56% (approximately).
or 55.56% (approximately).