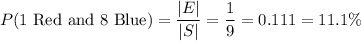Question

In a country X all markers are red or blue.In a box in country X there are 9 markers. I look at a random marker in the box and see that it is Blue. What is the probability that in the box there are 1 red and 8 blue markers

Answer 1

The probability that in the box there are 1 red and 8 blue markers is 0.111 or 11.1%

Solution-

In the box all markers are red or blue. There are total of 9 markers.

So the number of possible combination number of red or blue marker is,

`S=[(0,9),(1, 8),(2,7),(3,6),(4,5),(5,4),(6,3),(7,2),(8,1),(9,0)}]`

As at the random drawn, there was a Blue marker, so the condition of (9,0) i.e 9 Red marker and 0 Blue marker is not a case.

So the sample space becomes,

`S=[(0,9),(1, 8),(2,7),(3,6),(4,5),(5,4),(6,3),(7,2),(8,1)}]`

`|S|=9`

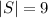
Let us assume that E is the event that in the box there are 1 red and 8 blue markers. So

`E=[(1,8)]`

`|E|=9`

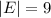
The probability that in the box there are 1 red and 8 blue markers is,

`P(\text{1 Red and 8 Blue})=(|E|)/(|S|)=(1)/(9)=0.111=11.1\%`