Answer:
The error is that, the student replaced i with -1 which is wrong as i = √-1
And he has replaced i^2 with 1 while i^2 = -1
Explanation:
Given two numbers that are being multiplied are:
(2-5i)(5+2i)
We will solve the question to get the right result so that the error can be detected.
So, multiplying both
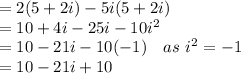
The error is that, the student replaced i with -1 which is wrong as i = √-1
And he has replaced i^2 with 1 while i^2 = -1