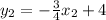For this case we have:
When two lines are parallel, their slopes are equal.
Be a line of the form
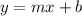
Where:
m is the slope
b is the cut point
If we have:
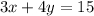
We can rewrite it as:
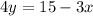
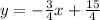
Thus, the slope of that line is given by
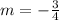
Since that line is parallel to the one we want to find, then
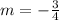 is the same for both lines.
is the same for both lines.
The equation of the line that we want to find follows the form:
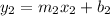
Where
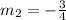
So, we have:
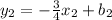
We have as data the point
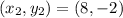 that passes through the line we want to find. Substituting the points we find the cut point
that passes through the line we want to find. Substituting the points we find the cut point
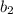 :
:
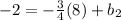
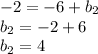
Thus, the equation of the requested line is given by:
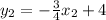
Answer: