Question

What are the x-intercepts of the graph of the function f(x)=x2+ 4x-12

Answer 1

x^2 + 4x-12 =0

factor

(x+6) (x-2)=0

x+6=0 x-2=0

x=-6 x=2

are the x intercepts

Answer -6, 2

Answer 2

The points are (-6,0) and (2, 0)

Explanation:

Given the function f(x)

`f(x)=x^2+ 4x-12`

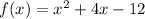
we have to find the x-intercepts of the graph of function.

x-intercepts are the x-coordinate of a point where a graph of function intersects the x-axis i.e the value of x at which the value of y is 0.

Hence, to find x-intercept we have to put the value of y=0 in f(x)

`x^2+ 4x-12=0`

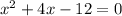
By middle term splitting method

`x^2-2x+6x-12=0`

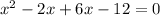
Taking x common from first two terms and 6 from last two terms

`x(x-2)+6(x-2)=0`

`(x+6)(x-2)=0`

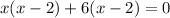
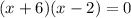
Using zero product property

⇒
`(x+6)=0\text{ or }(x-2)=0`

`x=-6\text{ or }x=2`

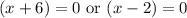
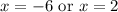
The points are (-6,0) and (2, 0)