Answer: The value of cosine is
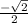 and the value of cotangent is -1.
and the value of cotangent is -1.
Step-by-step explanation:
The given point is
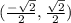 .
.
Since the x coordinate is negative and y coordinate is positive so the point must be lies in second quadrant.
The distance of the point from the origin is,
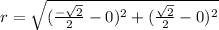
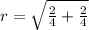
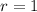
The given point is in the form of (a,b). So we get,
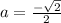
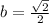
The formula for cosine,
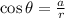
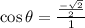
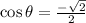
The formula for cotangent,
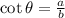
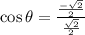
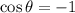
Therefore, the value of cosine is
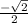 and the value of cotangent is -1.
and the value of cotangent is -1.