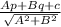Question

Find the distance from P to l. Line l contains points (-4,2) and (3,-5). Point P has coordinates (1,2). a. 55√5 , or appx 2.2 b. 67√7 , or appx 2.3 c. 52√2 , or appx 3.5 d. 103√3 , or appx 5.8

Answer 1

To Find: Distance between point P to line l

Solution: Points lying on line l are suppose A (-4,2) and B (3,-5).

Equation of line passing through (p,q) and (a,b) is given by the equation

→
`(y-a)/(x-b)=(p-a)/(q-b)`

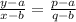
Equation of line AB is ,

→
`(y-2)/(x+4)=(-5-2)/(3+4)`

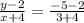
→y -2 = -1× (x +4)

→y -2 = -x -4

→x + y +4-2=0

→ x + y +2=0

Distance between point P (1,2) and line l whose equation is ,x+y+2=0 is given by=
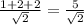`(1+2+2)/(√(2))=(5)/(√(2))`=5√2/2=3.535(approx)→Option (C)

→Which is given by the formula ,i.e if a line has equation , Ax + By +c=0 and we have to find the distance from (p,q) is given by =
`\frac{A p+ B q+ c}{\sqrt{A^(2)+B^(2)}}`