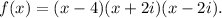Answer: The complete factorization of the given function over the field of complex numbers is
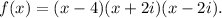
Step-by-step explanation: We are given to find the complete factorization of the following polynomial over the set of complex numbers :

We will be using the following formulas :
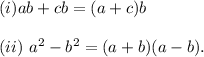
From (i), we have
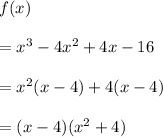
Now, to factorize completely, we will use the following value of imaginary number i(iota) :
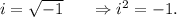
Therefore, we get
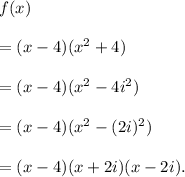
Thus, the complete factorization of the given function over the field of complex numbers is