Answer:
The interval notation for the domain is
![[(23)/(3),\infty ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/2zacyf6mmliyw05sjd1necrua5lo3ruv3b.png) .
.
Explanation:
Consider the provided information.
It is given that
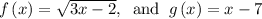
We need to find the value of
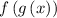 .
.
Put the value of g(x) in
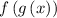 .
.
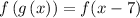 ....(1)
....(1)
Now, put x=x-7 in
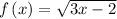
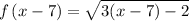
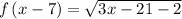
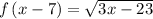
From equation 1.
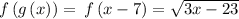
The domain of the function is the set of input values for which a function is defined.
Here, the value of
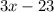 should be greater or equal to 0 as the square root of a negative number is not real.
should be greater or equal to 0 as the square root of a negative number is not real.
Domain=
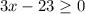
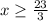
The value of x is all real number greater than
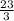 .
.
Hence, the interval notation for the domain is
![[(23)/(3),\infty ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/2zacyf6mmliyw05sjd1necrua5lo3ruv3b.png) .
.