Given :
Roscoe hit a ball straight up at a speed of 96 ft/s.
His bat hit the ball at a height 3 ft above the ground.
To Find :
After how many seconds did the ball hit the ground.
Solution :
When the ball reaches the same height from which it is thrown ( i.e. 3 ft ) its displacement will be zero.
So, using equation of motion :
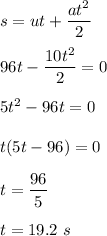
Now, time taken to reach ground from 3 feet of height is :
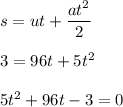
t = 0.03 s
Therefore, time taken is T = 19.2 + 0.03 = 19.23 seconds.