----------------------------------------------------------------------------------------------
Prerequisites:
----------------------------------------------------------------------------------------------
You need to know
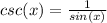
f(x) = A csc(ωx −ϕ)+B
A = Amplitude = |A|
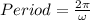
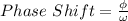
Y-Shift = B
Asymptotes of csc
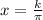
k = any constant integer number like -3, -2, -1, 0, 1, 2, 3...
Range of csc x
The ranges is from
![(-\infty,-1]U[1, \infty)](https://img.qammunity.org/2019/formulas/mathematics/college/8fxsgqq0te59dqo80ee7mqmvvtzjnfdoek.png)
------------------------------------------------------------------------------------------------------
Step By Step Explanation:
------------------------------------------------------------------------------------------------------
Find the Period of the function:
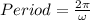
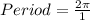

Find the Phase Shift
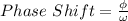
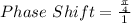
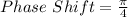
Find the Asymptotes
We know
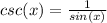 and when the denominator of
and when the denominator of
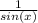 is equal to 0, we have an asymptote. So sin = 0 at k*pi .
is equal to 0, we have an asymptote. So sin = 0 at k*pi .
We know the asymptotes for
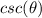 is where
is where
 .
.
The function that is presented has asymptotes at
 .+ Phase Shift.
.+ Phase Shift.
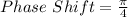

Now, just plugin an integer for k and you will find the asymptotes or you could say the asymptotes are at

Find the range.
We know the range for csc x =
![(-\infty,-1]U[1, \infty)](https://img.qammunity.org/2019/formulas/mathematics/college/8fxsgqq0te59dqo80ee7mqmvvtzjnfdoek.png) . Since we have a Y-Shift of -3, we have to adjust by subtracting -3 from 1 and -1.
. Since we have a Y-Shift of -3, we have to adjust by subtracting -3 from 1 and -1.
1 - 3 = -2
-1 - 3 = -4
New range =
![(-\infty,-4]U[-2, \infty)](https://img.qammunity.org/2019/formulas/mathematics/college/vcpxlp2owotw9nt6okln99p4yeg9wir1jy.png) .
.