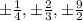Question

Which values are possible rational roots of 12x3+14x2−x+18=0 according to the rational root theorem? Select each correct answer. ±14 ±23 ±92 ±19

Answer 1

The correct ones are ±14 ±23 ±92

Answer 2

`\pm (1)/(4), \pm (2)/(3), \pm (9)/(2)`

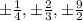
Explanation:

Given equation,

`12x^3 + 14x^2 - x + 18=0`

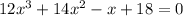
By the rational root theorem,

The possible roots of a polynomial are,

`\pm (\frac{\text{Factors of constant term}}{\text{Factors of leading coefficient}})`

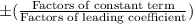
Here, the constant term = 18 and leading coefficient = 12,

∵ Factors of 18 = 1, 2, 3, 6, 9, 18,

Factors of 12 = 1, 2, 3, 4, 6, 12,

Thus, possible roots are,

`\pm ((1, 2, 3, 6, 9, 18)/(1, 2, 3, 4, 6, 12))`

`\pm (1, (1)/(2), (1)/(3), (1)/(4), (1)/(6), (1)/(12), 2, (2)/(3), 3, (3)/(2), , (3)/(4), 6, 9, (9)/(2), (9)/(4), 18)`

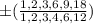
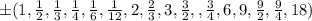
Hence, the correct answer are,

`\pm (1)/(4), \pm (2)/(3), \pm (9)/(2)`