Answer:
52.5°
Explanation:
Given : The ray XZ is the angle bisector of ∠WXY and m∠WXY = 105°.
To Find : The measure of ∠WXZ is ?
Solution:
∠WXY = 105°
The ray XZ is the angle bisector of ∠WXY
This means XZ divides the ∠WXY in two equal angles i.e. ∠WXZ and ∠ZXY
So, ∠WXY = ∠WXZ + ∠ZXY
∠WXY = 2∠WXZ
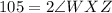
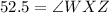
Hence The measure of ∠WXZ is 52.5°