Question

The ray XZ is the angle bisector of ∠WXY and m∠WXY = 105°. Enter m∠WXZ. The measure of ∠WXZ is

Answer 1

∠WXZ = 52.5°

∠WXY = 105°

and ∠WXY = ∠WXZ + ∠ZXY

∠WXZ =
`(105)/(2)` = 52.5°

Answer 2

52.5°

Explanation:

Given : The ray XZ is the angle bisector of ∠WXY and m∠WXY = 105°.

To Find : The measure of ∠WXZ is ?

Solution:

∠WXY = 105°

The ray XZ is the angle bisector of ∠WXY

This means XZ divides the ∠WXY in two equal angles i.e. ∠WXZ and ∠ZXY

So, ∠WXY = ∠WXZ + ∠ZXY

∠WXY = 2∠WXZ

`105 = 2 \angle WXZ`

`52.5 =\angle WXZ`

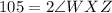
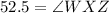
Hence The measure of ∠WXZ is 52.5°