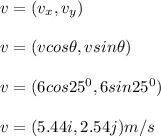Question

Puck 1 is moving 10 m/s to the left and puck 2 is moving 8 m/s to the right. They have the same mass, m.

a. What is the total momentum of the system before the collision? (Answer in terms of the mass, m.) (0.5 points)





b. What is the total momentum of the system after the collision? (Answer in terms of the mass, m.) (0.5 points)





c. Write puck 1's velocity after the collision in component form. (1 point)







d. What is the y-component of puck 2's velocity after the collision? (1 point)







e. What is the x-component of puck 2's velocity after the collision? (1 point)







f. At what angle does puck 2 move after the collision? Determine the angle and draw it on the diagram. (1 point)







g. What is the magnitude of puck 2's velocity after the collision? (1 point)

Answer 1

(a) the total momentum of the system before the collision = -2m kg.m/s.

(b) the total momentum of the system after the collision = -2m kg.m/s.

(c) puck 1's velocity after the collision in component form = (5.44 i, 2.54 j)

Step-by-step explanation:

Given;

mass of Puck 1 , = m

mass of Puck 2, = m (since they have the same mass m)

initial velocity of Puck 1, u₁ = 10 m/s to the left

initial velocity of Puck 2, u₂ = 8 m/s to the right

Let the rightward direction be positive direction

Let the leftward direction be negative direction

(a) the total momentum of the system before the collision;

P₁ = (initial momentum of Pluck 1) + (initial momentum of Pluck 2)

P₁ = (-mu₁) + mu₂

P₁ = mu₂ - mu₁

P₁ = m(u₂ - u₁)

P₁ = m(8 - 10)

P₁ = -2m kg.m/s

(b) the total momentum of the system after the collision;

Based on the principle of conservation of linear momentum, the total momentum before collision is equal to the total momentum after collision.

Thus, the total momentum of the system after the collision is -2m kg.m/s.

(c) puck 1's velocity after the collision in component form

`v = (v_x, v_y)\\\\v = (vcos \theta , vsin \theta)\\\\v = (6cos 25^0 , 6sin25^0)\\\\v = (5.44i, 2.54j)m/s`