Question

Solve the radical equation. square root of 8x+9=x+2

Which is an extraneous solution to the radical equation?


x = −1
x = 1
x = 5
There are no extraneous solutions to the equation.

Answer 1

D. There are no extraneous solutions to the equation.

Explanation:

We have been given an equation
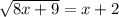`√(8x+9)=x+2`. We are asked to find extraneous solution to the radical equation.

First of all, we will square both sides of our given equation as:

`(√(8x+9))^2=(x+2)^2`

`8x+9=x^2+4x+4`

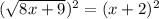
Upon switching the sides, we will get:

`x^2+4x+4=8x+9`

`x^2+4x-8x+4=8x-8x+9`

`x^2-4x+4=9`

`x^2-4x+4-9=9-9`

`x^2-4x-5=0`

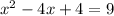
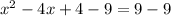
Upon splitting the middle term:

`x^2-5x+x-5=0`

`x(x-5)+1(x-5)=0`

`(x-5)(x+1)=0`

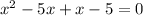
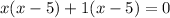
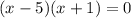
Using zero product property, we will get:

`(x-5)=0\text{ (or) }(x+1)=0`

`x=5 \text{ (or) }x=-1`

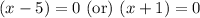
Now, we will check both solutions to find any extraneous solution as:

`√(8x+9)=x+2`

`√(8(-1)+9)=-1+2`

`√(-8+9)=1`

`√(1)=1`

`1=1` True.

`√(8x+9)=x+2`

`√(8(5)+9)=5+2`

`√(40+9)=7`

`√(49)=7`

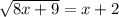
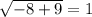
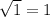
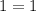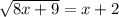
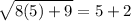
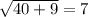
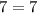`7=7` True.

Therefore, there is no extraneous solution to our given equation and option D is the correct choice.