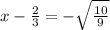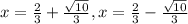Question

Solve for x.

3x^2-4x-2=0

Enter your simplified answers, as exact values, in the boxes

Answer 1

`x = (2)/(3) + (√(10) )/(3) , x = (2)/(3) - (√(10) )/(3)`

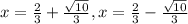
Explanation:

Multiplying the coefficient of x by the constant to get:

3 x (-2) = -6

Find factors of -6 that equal the middle term -4.

Since, no such factors can be found so we can solve the equation by completing the square.

To complete the square, divide the equation by the coefficient of x^2 which is 3 to get:

`x^(2) - (4)/(3) x - (2)/(3) = 0`

`x^(2) - (4)/(3) x = (2)/(3)`

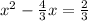
Now divide the coefficient of x by 2 and add the square of the result to both sides of the equation:

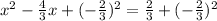
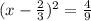
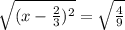
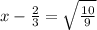`x^(2) - (4)/(3) x + (-(2)/(3) )^(2) = (2)/(3) +  (-(2)/(3) )^(2)`

`(x - (2)/(3) )^2 = (2)/(3) + (4)/(9)`

`(x - (2)/(3) )^2 = (4)/(9)`

`\sqrt{(x - (2)/(3) )^2} = \sqrt{(4)/(9) }`

`x - (2)/(3) = \sqrt{(10)/(9) }` ,
`x - (2)/(3) = -\sqrt{(10)/(9) }`

`x = (2)/(3) + (√(10) )/(3) , x = (2)/(3) - (√(10) )/(3)`

Answer 2

ANSWER


`x=\frac{2-√(10)} {3}`

or


`x=\frac{√(10)+2} {3}`

We have


`3x^2-4x-2=0`

Since we cannot factor easily, we complete the square.

Adding 2 to both sides give,


`3x^2-4x=2`

Dividing through by 3 gives


`x^2-(4)/(3)x= (2)/(3)`

Adding
`(-(2)/(3))^2` to both sides gives


`x^2-(4)/(3)x+(-(2)/(3))^2= (2)/(3)+(-(2)/(3))^2`

The expression on the Left Hand side is a perfect square.


`(x-(2)/(3))^2= (2)/(3)+(4)/(9)`


`\Rightarrow (x-(2)/(3))^2= (10)/(9)`


`\Rightarrow (x-(2)/(3))=\pm \sqrt{(10)/(9)}`


`\Rightarrow (x)=(2)/(3) \pm {(√(10))/(3)`

Splitting the plus or minus sign gives


`x=\frac{2- √(10)} {3}`

or


`x=\frac{√(10)+2} {3}`