Question

15.
Can someone help me?​

Answer 1

The radius, in inches, of the base of the cone will be:

r = 6 inches

Hence, option B is correct.

Explanation:

Given

The Volume of a right circular cone V = 24 π cubic inches

The height of the cone h = 2 inches

To determine

The radius of the base of the cone r = ?

Using the formula involving Volume m, height h, and radius r of a right circular cone.

`V\:=(1)/(3)h\:\pi \:\:r^2\:`

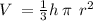
substituting V = 24 π, h = 2 to find the radius r

`\left(24\pi \right)=(1)/(3)\left(2\right)\:\pi \:r^2`

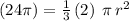
switch sides

`(1)/(3)\left(2\right)\pi r^2=\left(24\pi \right)`

`(1)/(3)2\pi r^2=24\pi`

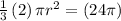
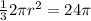
simplify

`2\pi r^2=72\pi`

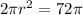
Divide both sides by 2π

`(2\pi r^2)/(2\pi )=(72\pi )/(2\pi )`

`r^2=36`

`\mathrm{For\:}x^2=f\left(a\right)\mathrm{\:the\:solutions\:are\:}x=√(f\left(a\right)),\:\:-√(f\left(a\right))`

`r=√(36),\:r=-√(36)`

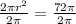
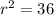
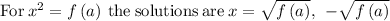
Thus,

`r=6,\:r=-6`

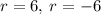
As we know that the radius can not be negative.

Therefore, the radius, in inches, of the base of the cone will be:

• r = 6 inches

Hence, option B is correct.