Question

Could 10.6\text{ cm}, 5.6\text{ cm},10.6 cm,5.6 cm,10, point, 6, space, c, m, comma, 5, point, 6, space, c, m, comma and 4.0\text{ cm}4.0 cm4, point, 0, space, c, m be the side lengths of a triangle?

Answer 1

No.

Step-by-step explanation: Khan Academy

Answer 2

Since we know that triangle inequality theorem states that sum of any two sides of a triangle must be greater than third side.

Now let us see if it is true for our given side lengths.

`10.6+5.6>4.0`

`16.2>4.0`

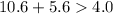
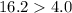
Now let us try with another pair.

`5.6+4.0>10.6`

`9.6<10.6`

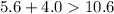
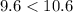
We can see that sum of 5.6 and 4 is less than 10.6. Therefore, 10.6 cm, 5.6 cm and 4.0 cm can not be side lengths of a triangle.