Answer:
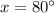
Explanation:
Solution 1:
Recall that in an isosceles triangle, the two angles adjacent to the congruent sides are equal. Since the sum of interior angles in a triangle add up to
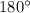 , we set up the following equation:
, we set up the following equation:
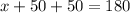 .
.
Solving, we get:
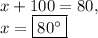 .
.
Solution 2:
The Law of Sines states:
 , for any triangle.
, for any triangle.
We can use this to set up a proportion with the information given:
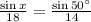 .
.
Solving, we get:
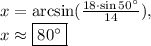 .
.