This is loaded question, but let me take a stab at it:
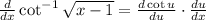
with
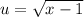
Start with the first part of the chain rule term:
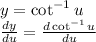
because cot^-1 is inverse to cot we also know that
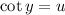
and use it in the earlier equation:
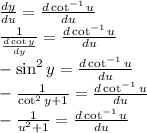
Now, the second term of the chain rule:

Putting it together:
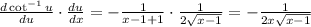
and that is the final derivative of your expression.