Answer:
The period of Y increases by a factor of
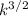 with respect to the period of X
with respect to the period of X
Explanation:
The equation
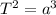 shows the relationship between the orbital period of a planet, T, and the average distance from the planet to the sun, A, in astronomical units, AU. If planet Y is k times the average distance from the sun as planet X, at what factor does the orbital period increase?
shows the relationship between the orbital period of a planet, T, and the average distance from the planet to the sun, A, in astronomical units, AU. If planet Y is k times the average distance from the sun as planet X, at what factor does the orbital period increase?
For the planet Y:
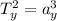
For planet X:

To know the factor of aumeto we compared
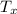 with
with

We know that the distance "a" from planet Y is k times larger than the distance from planet X to the sun. So:
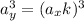
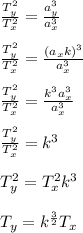
Finally the period of Y increases by a factor of
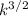 with respect to the period of X
with respect to the period of X