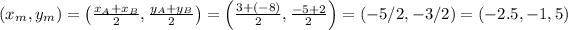Answer:
The center of the circle is the point
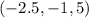 , that can be written as
, that can be written as
 .
.
Explanation:
Here we will need some facts from elementary geometry, and other from the geometric representation of complex numbers.
Geometrical representation of complex numbers. Recall that a complex number
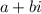 can be identified with a point in the plane: the point with coordinates
can be identified with a point in the plane: the point with coordinates
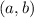 .
.
So, the number
 ‘‘is’’ the point
‘‘is’’ the point
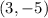 , and
, and
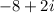 ‘‘is’’ the point
‘‘is’’ the point
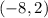 .
.
Elementary geometry. The center of a circle is the midpoint of all its diameters.
Now, as the diameter of the circle has endpoints
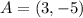 and
and
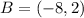 , we only need to find the midpoint of the segment AB. Form analytic geometry we know that this can be done by the formulas,
, we only need to find the midpoint of the segment AB. Form analytic geometry we know that this can be done by the formulas,