Question

Given △ABC. m∠A>m∠B>m∠C. Perimeter=30. Which side of △ABC may have length 7?

Answer 1

In △ABC with angles following m∠A > m∠B > m∠C and a perimeter of 30, side AB opposite the smallest angle C may have length 7.

Step-by-step explanation:

In a triangle △ABC where the angle measures follow m∠A > m∠B > m∠C, the side lengths are inversely related to the angle measures. This means the longest side is opposite the largest angle, and the shortest side is opposite the smallest angle. Therefore, since m∠A is the largest, side BC - which is opposite angle A - would be the longest. As m∠B is greater than m∠C, side AC would be longer than side AB. With a perimeter of 30, if one side is 7, it must be the shortest side because the sum of the lengths of the two other sides must be 23 to meet the perimeter requirement. So, the side which may have a length of 7 is AB, which is opposite the smallest angle, angle C.

Answer 2

As given in △ABC,

`m\angle A>m\angle B>m\angle C`

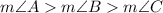
As from the properties of trigonometry we know that, the greater the angle is, the greater is the value of its sine. i.e

`\sin A>\sin B>\sin C`

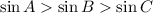
According to the sine law,

`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

In order to make the ratio same, even though m∠A>m∠B>m∠C, a must be greater than b and b must be greater than c.

`\Rightarrow a>b>c`

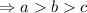
Also given that its perimeter is 30. Now we have to find out whose side length is 7. So we have 3 cases.

Case-1. Length of a is 7

As a must be the greatest, so b and c must be less than 7. Which leads to a condition where its perimeter won't be 30. As no 3 numbers less than 7 can add up to 30.

Case-2. Length of b is 7

As b is greater than c, so c must 6 or less than 6. But in this case the formation of triangle is impossible. Because the triangle inequality theorem states that the sum of any 2 sides of a triangle must be greater than the measure of the third side. If b is 7 and c is 6, then a must be 17. So no 2 numbers below 7 can add up to 17.

Case-3. Length of c is 7

As this is the last case, this must be true.

Therefore, by taking the aid of process of elimination, we can deduce that side c may have length 7.