Question

The John Deere company has found that revenue, in dollars, from sales of heavy-duty tractors is a function of the unit price p, in dollars, that it charges. If the revenue R is R(p)=-1/2 p^2+1900p, please answer the following questions:

Part A: How much revenue will the company generate if they sell 700 tractors?

Part B: How many tractors does the company want to sell to maximize the revenue?

Show your work/explain your answers please!

Answer 1

A- 700 tractors will generate a revenue of $1,085,000

B- The company must sell 1900 tractors in order to maximize the revenue.

Solution-

The John Deere company has found that the revenue from sales of heavy-duty tractors is a function of the unit price p, in dollars, that it charges. If the revenue R, in dollars, is

`R(p)=-(1)/(2)p^2+1900p`

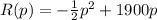
How much revenue will the company generate if they sell 700 tractors:

`\Rightarrow R(p)=-(1)/(2)(700)^2+1900(700)`

`\Rightarrow R(p)=1,085,000`

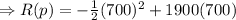
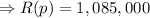
Therefore, 700 tractors will generate a revenue of $1,085,000

How many tractors does the company want to sell to maximize the revenue

By calculating the value of p for which R(p) is maximum will be the number of tractors for which the revenue will be maximum. We can take the help of derivatives to find this.

`R(p)=-(1)/(2)p^2+1900p`

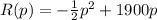
Taking the derivative w.r.t p,

`\Rightarrow R' (p)=-(1)/(2)* 2* p+1900`

`\Rightarrow R' (p)=-p+1900`

`\Rightarrow R' (p)=1900-p`

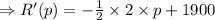
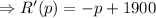
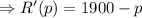
Taking R'(p) = 0, to find out the critical points

`\Rightarrow R' (p)=0`

`\Rightarrow 1900-p=0`

`\Rightarrow p=1900`

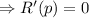
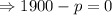
So, at p = 1900, the function R(p) will be maximum. The maximum value will be,

`\Rightarrow R(p)=-(1)/(2)(1900)^2+1900(1900)`

`\Rightarrow R(p)=1,805,000`

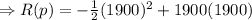
Therefore, the company must sell 1900 tractors in order to maximize the revenue and the maximum revenue will be $1,805,000.