Answer-
A- 700 tractors will generate a revenue of $1,085,000
B- The company must sell 1900 tractors in order to maximize the revenue.
Solution-
The John Deere company has found that the revenue from sales of heavy-duty tractors is a function of the unit price p, in dollars, that it charges. If the revenue R, in dollars, is
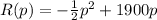
How much revenue will the company generate if they sell 700 tractors:
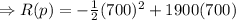
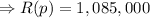
Therefore, 700 tractors will generate a revenue of $1,085,000
How many tractors does the company want to sell to maximize the revenue
By calculating the value of p for which R(p) is maximum will be the number of tractors for which the revenue will be maximum. We can take the help of derivatives to find this.
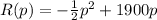
Taking the derivative w.r.t p,
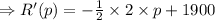
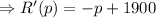
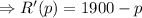
Taking R'(p) = 0, to find out the critical points
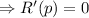
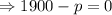
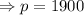
So, at p = 1900, the function R(p) will be maximum. The maximum value will be,
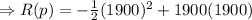
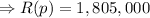
Therefore, the company must sell 1900 tractors in order to maximize the revenue and the maximum revenue will be $1,805,000.