Question

For what value(s) of k will the relation not be a function

R={(k-8.3+2.4k,-5),(-(3)/(4)k,4)}
S = (2−
I WILL RATE AND PUT BRAINILEST ANSWER

Answer 1

We are given two relations

(a)

Relation (R)

`R=[((k-8.3+2.4k),-5),(-(3)/(4)k,4)]`

We know that

any relation can not be function when their inputs are same

so, we can set both x-values equal

and then we can solve for k

`k-8.3+2.4k=-(3)/(4) k`

`3.4k-8.3=-(3)/(4)k`

`3.4k\cdot \:10-8.3\cdot \:10=-(3)/(4)k\cdot \:10`

`4k-83=-(15)/(2)k`

`34k=-(15)/(2)k+83`

`(83)/(2)k=83`

`83k=166`

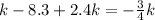
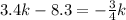
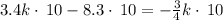
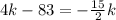
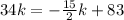
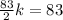
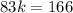
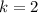`k=2`............Answer

(b)

S = (2−

We know that

any relation can not be function when their inputs are same

so, we can set both x-values equal

and then we can solve for k

`2-|k+1|=-6`

`2-\left|k+1\right|-2=-6-2`

`-\left|k+1\right|=-8`

`\left|k+1\right|=8`

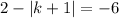
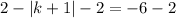
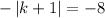
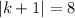
Since, this is absolute function

so, we can break it into two parts

`|f\left(k\right)|=a\quad \Rightarrow \:f\left(k\right)=-a\quad \mathrm{or}\quad \:f\left(k\right)=a`

`k+1=-8\quad \quad \mathrm{or}\quad \:\quad \:k+1=8`

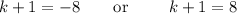
we get

`k+1=-8\quad`

`k=-9`

`k+1=8\quad`

`k=7`

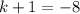
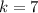
so,

`k=-9\quad \mathrm{or}\quad \:k=7`...............Answer