We are given two relations
(a)
Relation (R)
![R=[((k-8.3+2.4k),-5),(-(3)/(4)k,4)]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/d02kf9n21hocnpm5btc4j5845vlm14ayft.png)
We know that
any relation can not be function when their inputs are same
so, we can set both x-values equal
and then we can solve for k
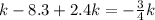
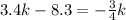
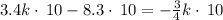
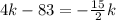
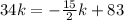
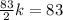
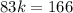
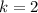 ............Answer
............Answer
(b)
S = (2−
We know that
any relation can not be function when their inputs are same
so, we can set both x-values equal
and then we can solve for k
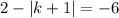
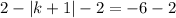
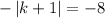
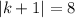
Since, this is absolute function
so, we can break it into two parts
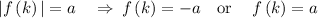
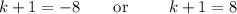
we get
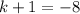
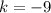
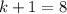
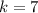
so,
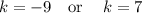 ...............Answer
...............Answer