ANSWER
ANSWER TO QUESTION 1.
If you give
 surfing lessons, then you will earn $
surfing lessons, then you will earn $

If you are charged $200 for using the place, then your profit will reduce by $200.
The profit function is given by
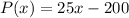 dollars.
dollars.
The y-intercept is
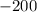 . It is negative because it is a cost which is a liability. So it does not add to your profit.
. It is negative because it is a cost which is a liability. So it does not add to your profit.
ANSWER TO QUESTION 2.
The slope is
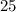 . It is positive because as the number of hours increases, the profit earned also increases. In other words there is a direct relation between the number of hours worked and the profit earned.
. It is positive because as the number of hours increases, the profit earned also increases. In other words there is a direct relation between the number of hours worked and the profit earned.
ANSWER TO QUESTION 3.
The slope intercept form is when an equation is written in the form;
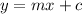 ,
,
where
 is the slope and
is the slope and
 is the y-intercept. The profit function in slope intercept form is
is the y-intercept. The profit function in slope intercept form is
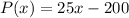
ANSWER TO QUESTION 4.
If you break even, then the difference between the revenue and cost is zero. So we equate the profit function to zero.
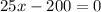
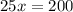
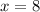
Therefore you need to give 8 different lessons to break even.
ANSWER TO QUESTION 5.
If you give 20 lessons, the
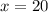 . We need to substitute
. We need to substitute
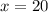 in to the profit function to calculate the profit made after 20 lessons.
in to the profit function to calculate the profit made after 20 lessons.
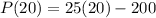
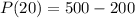
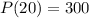 .
.
ANSWER TO QUESTION 6.
If the new price is $75, then the new profit function becomes
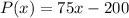
ANSWER TO QUESTION 7.
To find the number of lessons that lets you break even, we equate the new profit function to zero.
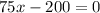
We solve for x by adding 200 to both sides of the equation.
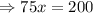
We now divide through by 75
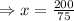

Therefore you would have to 2\frac{2}{3} lessons to break even. That is approximately 3 lessons.
ANSWER TO QUESTION 8.
If you give 20 lessons and we want to find the profit you made with this new profit function, then we have to plug in
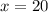 in to
in to
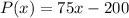 .
.
That is,

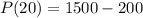
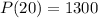 dollars
dollars