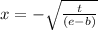Answer:
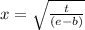 ,
,

Explanation:
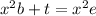
To solve this equation for x, arrange the like terms together by placing the two terms with variable
 at one side of the equation and the remaining terms at the other side of the equation:
at one side of the equation and the remaining terms at the other side of the equation:
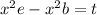
Now take the common terms out and write it as:
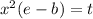
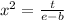
Now take square root on both sides:

 ,
,