Question

In a study of government financial aid for college​ students, it becomes necessary to estimate the percentage of​ full-time college students who earn a​ bachelor's degree in four years or less. Find the sample size needed to estimate that percentage. Use a 0.02 margin of error and use a confidence level of 90​%.

Assume that nothing is known about the percentage to be estimated. n= ​(Round up to the nearest​ integer.)

Answer 1

Answer:100. Step-by-step explanation round to to nearest 10

Answer 2

Answer: 1692

Explanation:

if prior estimate of proportion is not known , then the formula to find the sample size is given by:-

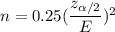`n=0.25((z_(\alpha/2))/(E))^2` (1)

For 90% confidence interval , significance level =
`\alpha=1-0.90=0.10`

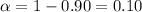
Critical value =
`z_(\alpha/2)=1.645`

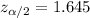
Margin error = 0.02

Now, substitute all the above values in (1), we get

`n=0.25((1.645)/(0.02))^2=1691.265625\approx1692`

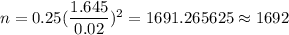
Hence, the required minimum sample size should be 1692.