Answer:
The system of equations that could be used to find the cost of one adult ticket and one child ticket is:
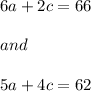
On solving we get:
Cost of one adult ticket= $ 10
and cost of one child ticket= $ 3
Explanation:
a denote the cost of one adult ticket.
and c denote the cost of one child ticket.
Roy buys 6 adult tickets and 2 child tickets for a total of $66.
i.e. the equation that could be written is:
6a+2c=66-----------(1)
and also Elisa buys 5 adult tickets and 4 child tickets for a total of $62.
This means that the equation that is obtained from this information is:
5a+4c=62--------------(2)
Also, on solving the two equations by the method of elimination
we multiplying equation (1) by 2 and subtract both the equations we get:
12a+4c=132
and 5a+4c=62
-----------------------------------
7a=70
i.e. a=10
and on putting the value of a in equation (1) we get:
60+2c=66
i.e. 2c=66-60
i.e. 2c=6
i.e. c=3
Hence, the cost of one adult ticket=$ 10
and cost of one child ticket= $ 3